A quadrilateral and an internal point from which four line segments are drawn, each parallel to a different side. What is blue : orange?
Categories
A limited scope
Month: February 2025
Categories
Rectangular justice
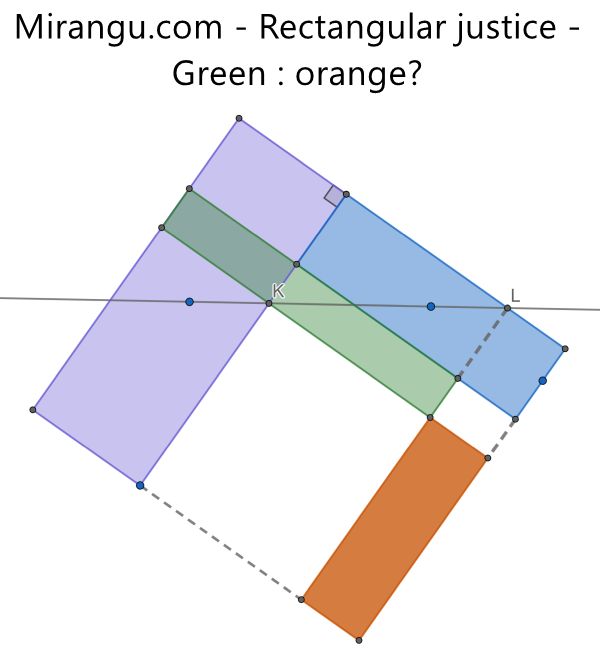
Purple and blue rectangles with line KL connecting their centers. What is the area ratio Green:Orange?
Categories
Right angle II
A rectangle with several line segments. What’s the angle α?
Categories
Cocked hats
Three squares and a right triangle. How are the green, orange, and blue areas related?
Categories
Eye of Providence
A regular pentagon and an equilateral triangle. What is the angle α?
Categories
Party mask
Touching green and blue circles are connected by an orange semicircle whose ends are C on the green circle and E, the center of the blue circle. C, A, B are collinear, and D is on both the green circle and the semicircle. Show that the circle (CDB) is tangent to the blue circle at B.
Categories
Velocipede IV
Two circles with three common tangents. The smaller radius is extended as shown. Express the extension length x in terms of R and r.
Categories
Egyptian sunset II
Three equilateral triangles with areas 1, x and x² fit inside a semicircle. What is x?
Categories
Moving boxes
Five squares inside a square. Prove that the three red vertices are collinear.
Categories
Overburdened
A fixed red circle hovers centered above a fixed segment AB, with relative dimensions as shown. Determine the quotient of areas blue/green, and show that it does not depend upon the choice of the point J on the red circle.