Circles touch on the left, their rightmost points bisected by a perpendicular line. A circle, centered on that perpendicular, divides the one circle equally (red versus green). Show that the other circle is also divided equally.
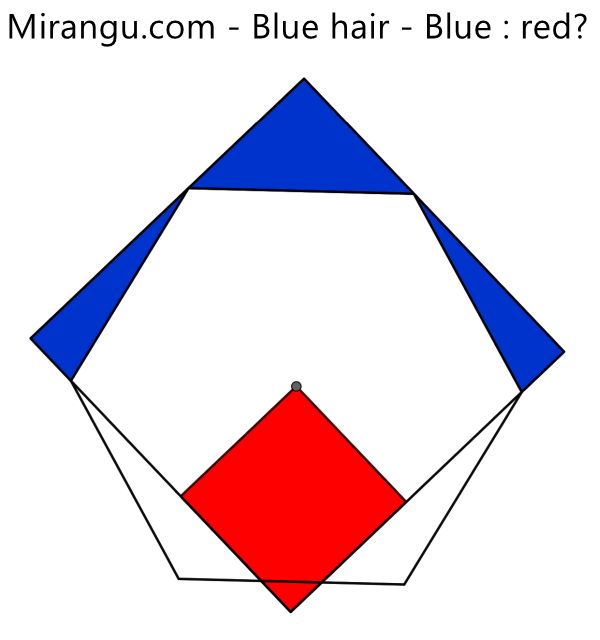
A regular hexagon and two squares. The centre of the hexagon is a vertex of the smallest square. What is blue : red?
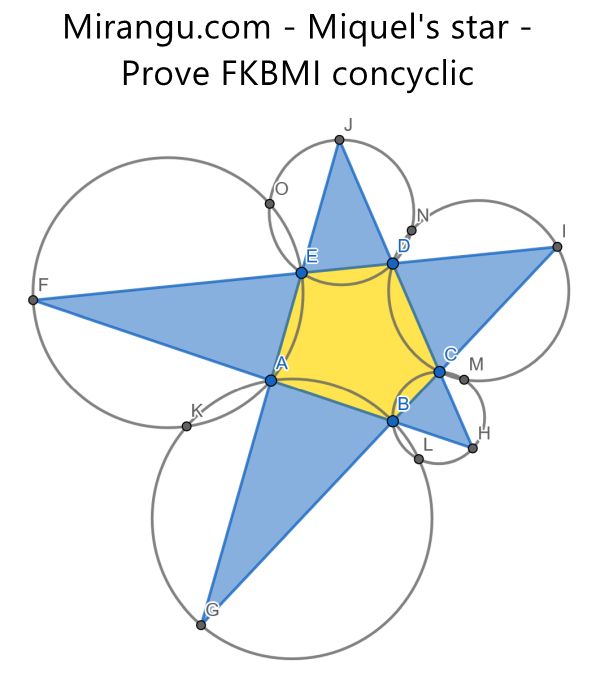
A convex pentagon ABCDE with extended sides and five circles connecting vertices and intersections. Prove that FKBMI are concyclic. Bonus question: prove KLMNO concyclic.
Rigid sticks of lengths p, m, and n attach to balloons as tangent lines meeting at a common point G. What is the center of the circle that is the locus of other G-like-points with the same sum p2+ m2 + n2?
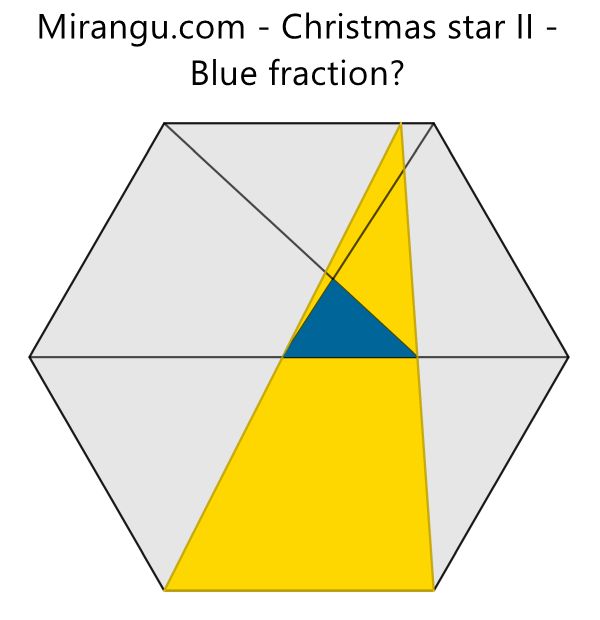
A regular hexagon and several line segments. What fraction is blue?
Green and red lines of lights go up the tree, each segment projected from one of the two red and green anchors on the ground. Show that the purple lines meet on the ground, and also the orange lines meet on the ground.
Four squares and a regular hexagon. A circle with two tangents. Show that the circle is tangent to the hexagon circumcircle. Note that the right dotted tangency point does not lie on the hexagon side.
Triangle ABC with cevians crossing at D. Ends of cevians form a triangle EFG. Sides FG and BC intersect at H. I and J are defined similarly. Show that H, I, and J are collinear.
Three semicircles and one radius. The coloured semicircles are tangent and the shown radius is the common tangent. Prove that the radii of the semicircles are a geometric sequence (so in proportion 1 : x : x²) and find x.
Two squares and a rectangle. Prove that the four red points are concyclic.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now