An equilateral triangle with a cevian and an inscribed circle. Prove that the red tangency points and midpoint are collinear.
Categories
Stuck boulder II
Month: October 2024
Categories
The epaulettes
A triangle and its incircle. Prove that the two coloured triangles are similar.
Categories
Two-story pyramid with shadows
The blue pyramid casts a dark green shadow, which magically appears, reversed, on the above ground floor (halfway up). Show that there is a point that is always on the red line, no matter the time of day.
Categories
The dumbbell
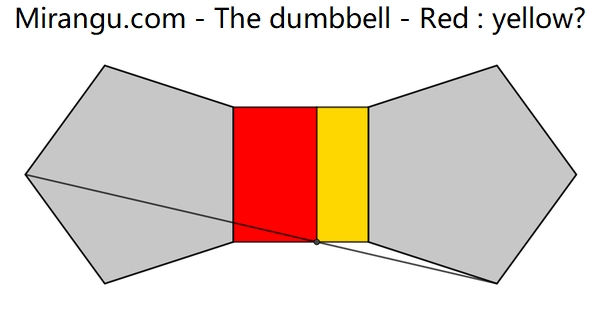
A square and two regular pentagons. What is red : yellow?
Categories
On all fours
Four coupled squares. Prove that the green and red quadrilateral have equal areas.
Categories
Mitosis
A triangle is divided by a cevian into two triangles (diagram not to scale). If those two triangles are similar, what can we tell about the original triangle?
Categories
Avocado
An orange circle meets a green semicircle, with two segment bisections marked in the diagram. Show that the red segments have the same length, and the blue segments have the same length.
Categories
Hawfinch III
A circle, two tangents, a chord and a secant. Prove that α=β.
Categories
Planks in the eye
Equal sides of a triangle touch concentric circles, the third side containing the common center. Show that red * dotted_purple = orange * dark_blue !
Categories
Kissing squares
Two squares share a vertex. Prove that the three green points are collinear.