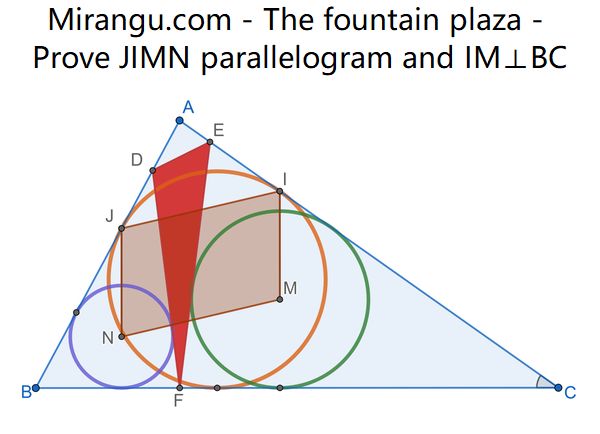
The incircle of ABC touches sides at I and J. D, E, F are the bases of altitudes from C, B, and A. The incenters of BDF of CEF are N and M, respectively. Show that JIMN is a parallelogram and that IM is perpendicular to BC.
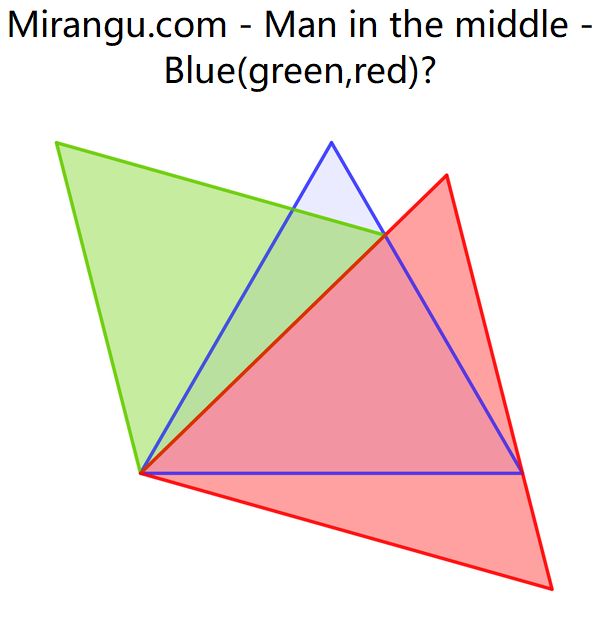
Three equilateral triangles share a vertex. What is the area of the blue one in terms of green and red?
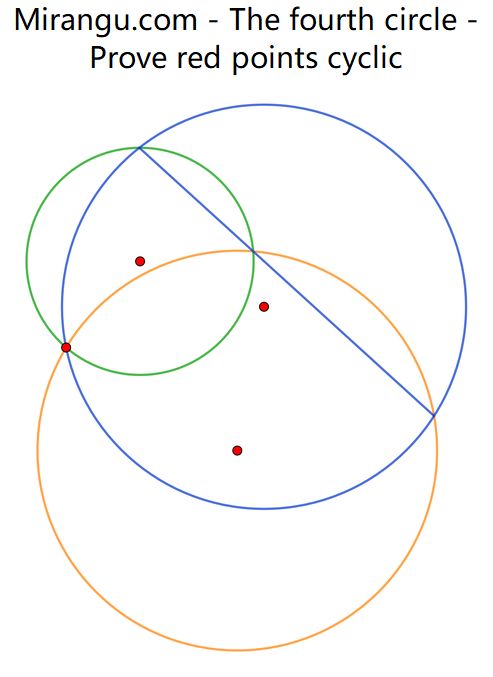
Three circles and a line segment connecting three intersections. Prove that the three centres and the common intersection are concyclic.
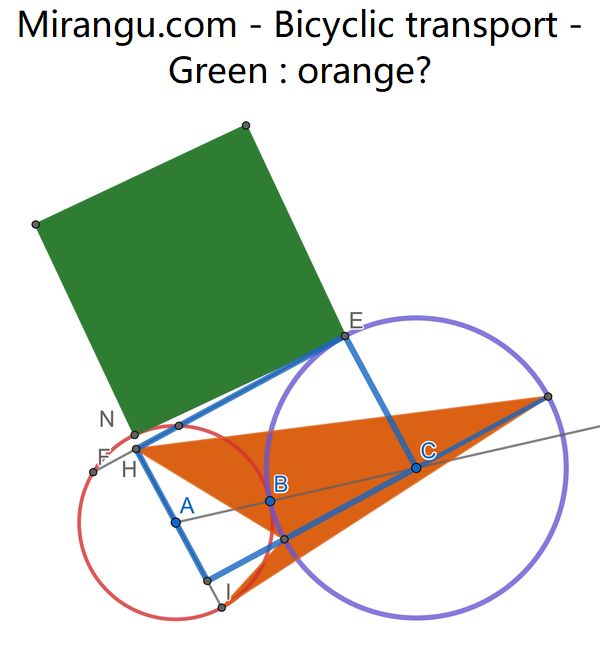
EHF is tangent to the purple circle at E, and EN is tangent to the red circle at N. A and C are the circle centers. A blue rectangle has three corners HEC and the point A on one side. What is the ratio of areas, green square to orange quadrilateral?
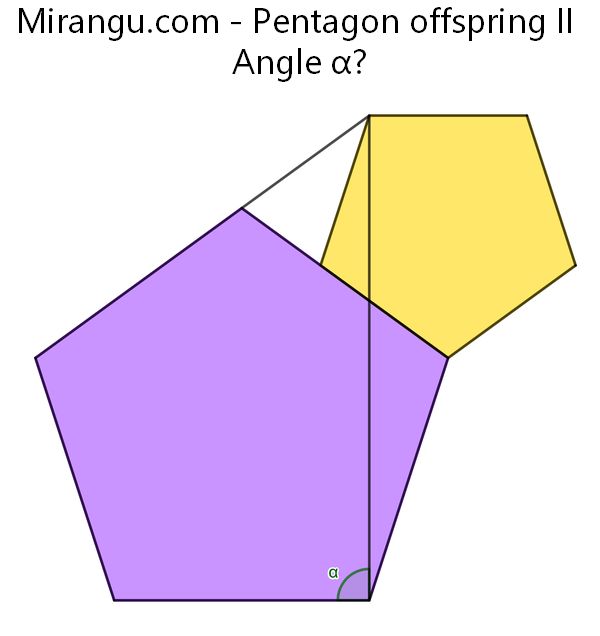
Two regular pentagons, one of which has an extended side. What’s the angle α?
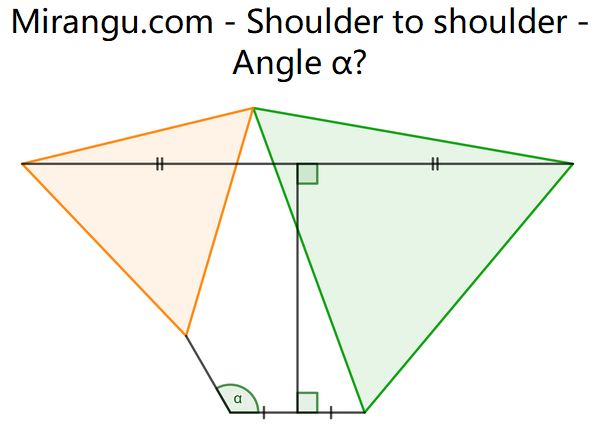
Two equilateral triangles sharing a vertex and several line segments. What’s the angle α?
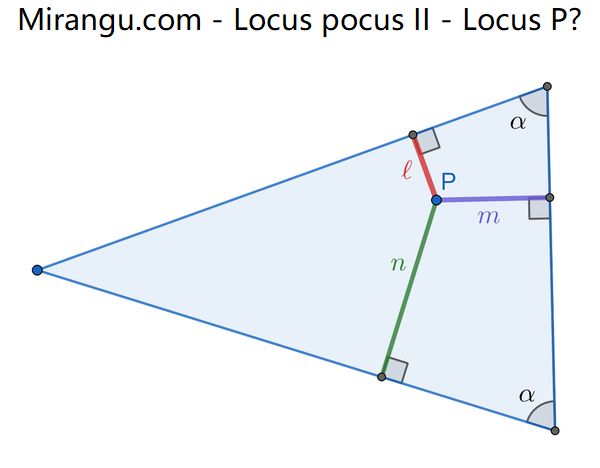
What is the locus of points P for which perpendicular lengths (red=l, green=n, purple=m) to the sides of an isosceles triangle satisfy the condition red*green = purple2?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now