A circle and several triangles. Prove that the green triangle is isosceles.
The silly walk
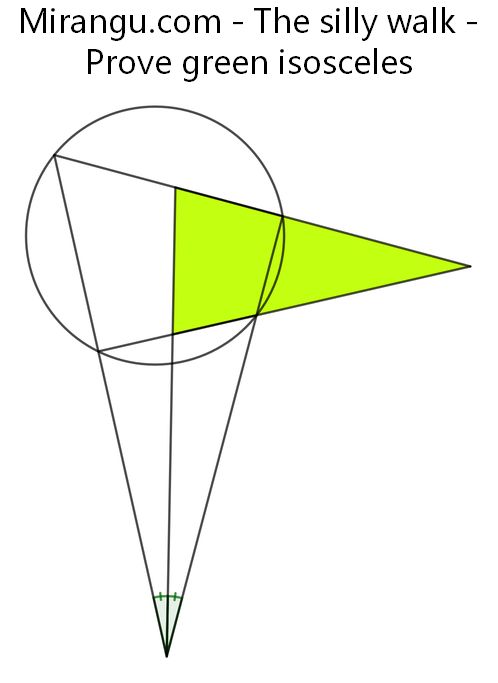

A circle and several triangles. Prove that the green triangle is isosceles.
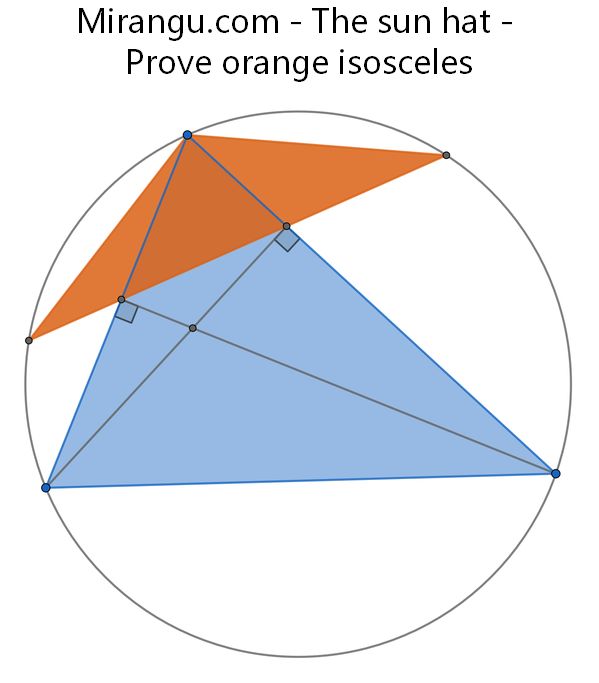
Two triangles share a circumcircle and vertex, with one edge of the orange triangle containing the feet of two of the altitudes of the blue triangle. Show that the orange triangle is isosceles.
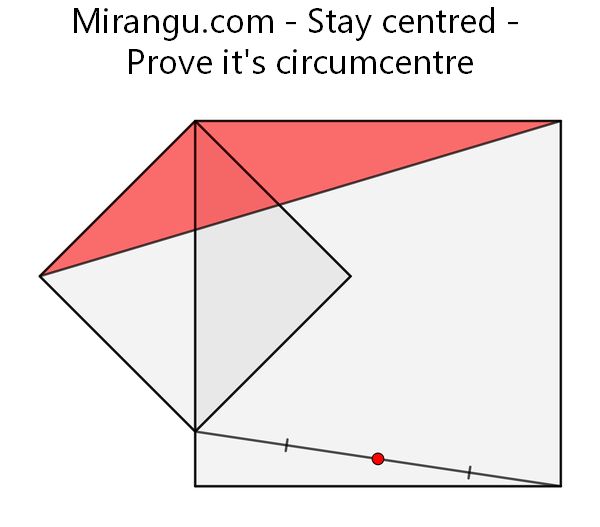
Two squares share a vertex. Prove that the red point is the circumcentre of the red triangle.
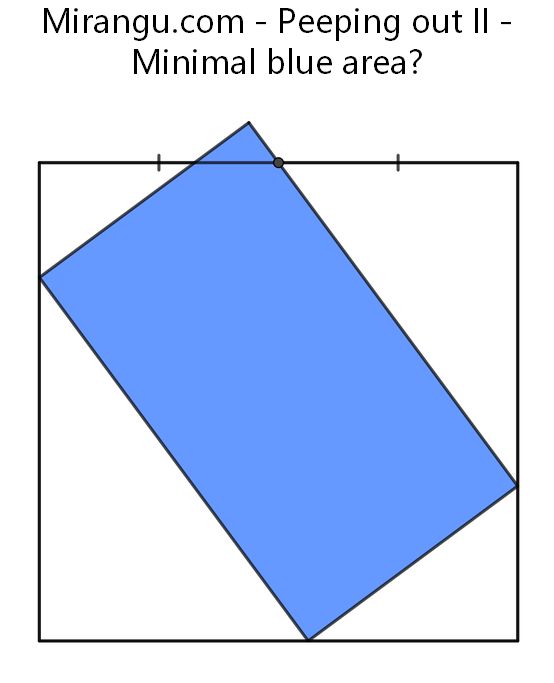
A unit square and a rectangle touching three square sides and passing through the midpoint of the upper side. What is the minimal blue area?
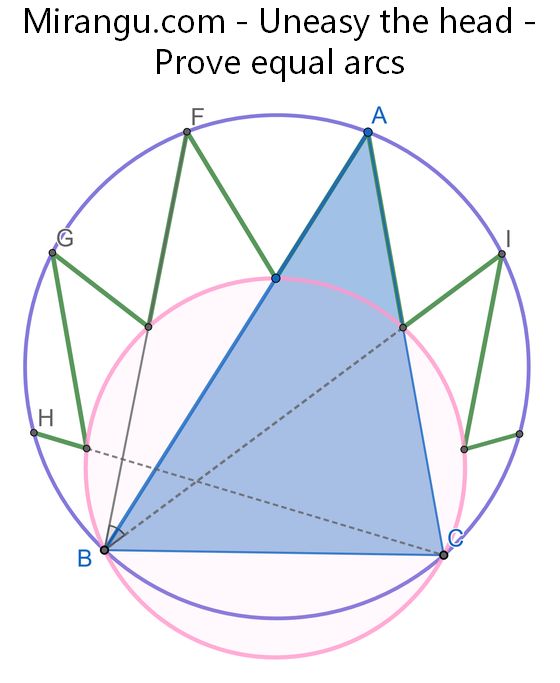
The green zigzag crown segments would extend through either B or C. Show that the arcs along the top are equally spaced.
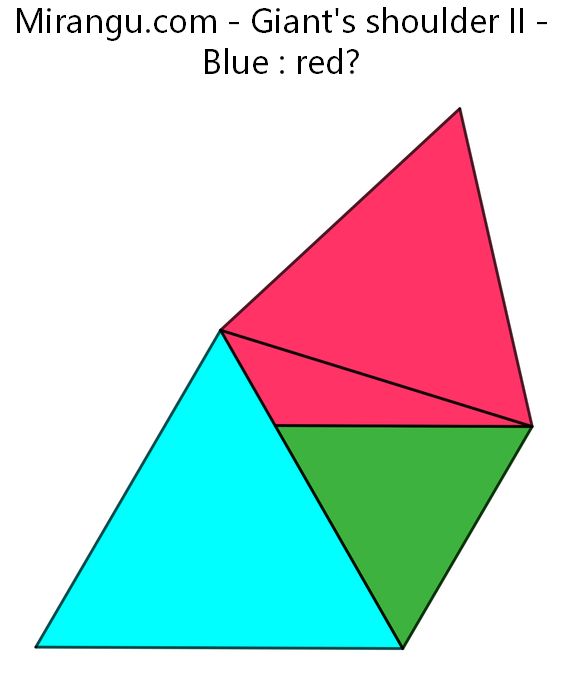
Three equilateral triangles share three vertices. What is blue : red?
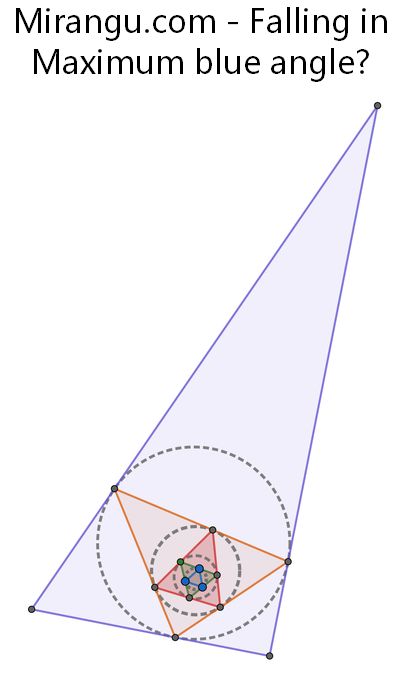
Start with an acute triangle and form a new triangle from the points of tangency of its inscribed circle. Continue this process to make make the triangle with blue vertices. What is the maximum possible angle at a blue vertex?
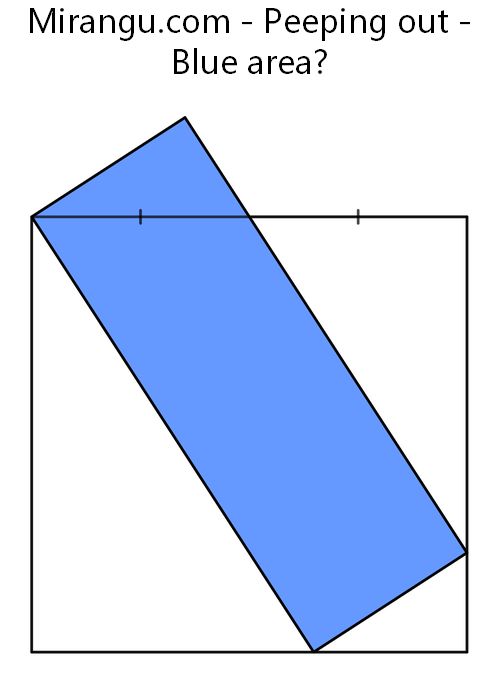
A unit square and a rectangle. What is the blue area?
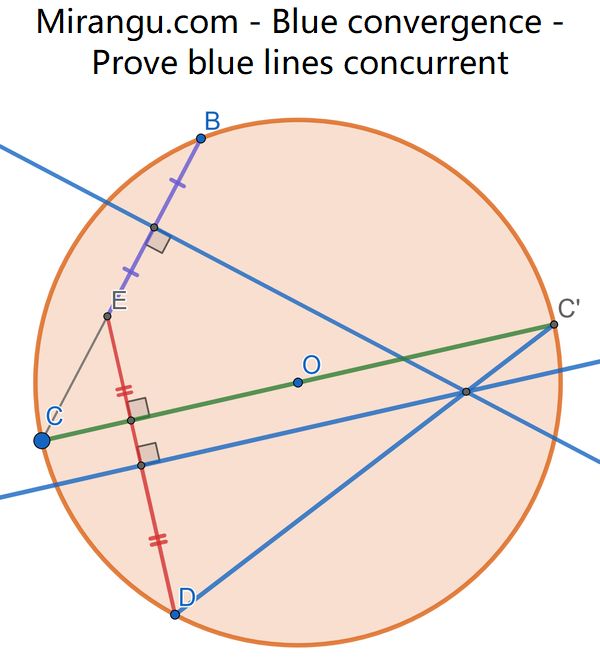
Points B, C, D are on a circle with centre O and diameter COC’. Point E is on the line BC such that DE is perpendicular to COC’. Show that the perpendicular bisectors of EB and ED and the line DC’ are concurrent.
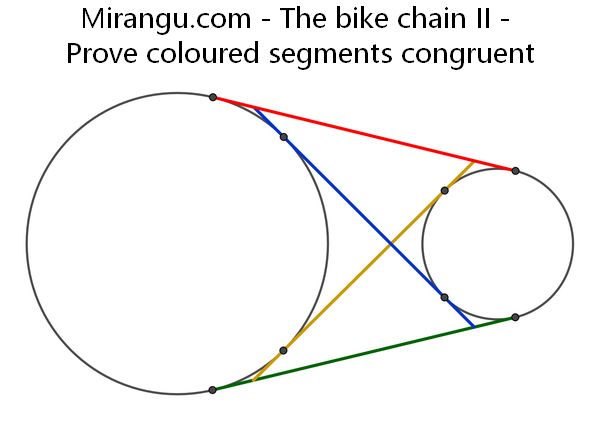
Two circles and four coloured common tangents. Prove they are congruent.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now