What is the ratio orange/green?
Angle versus height
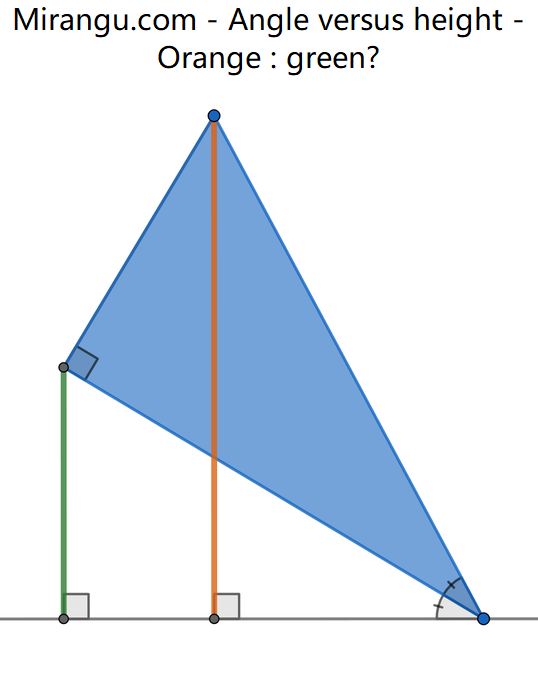

What is the ratio orange/green?
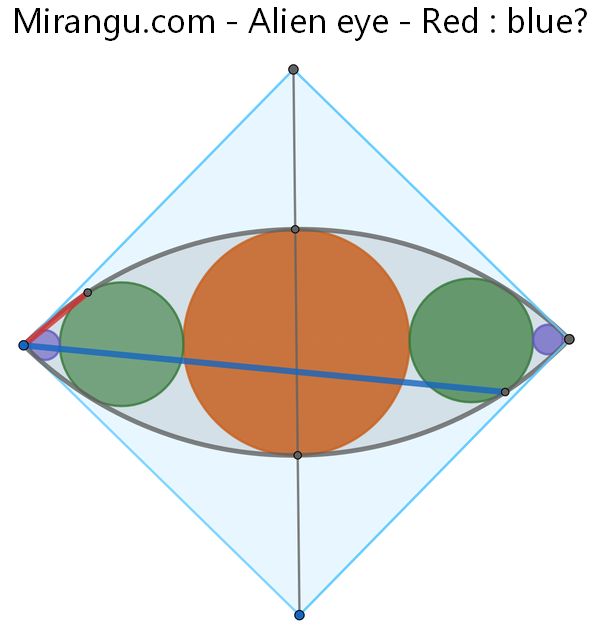
Two quarter-circles fit inside a square, and five circles fit inside the overlapped region, centred. What is the ratio of the (straight line) segment lengths red to blue? (The segments connect to points of tangency.)
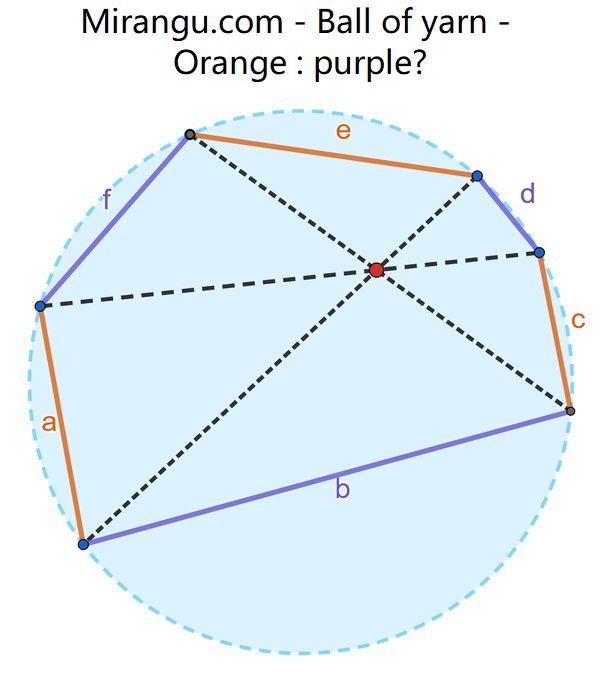
A cyclic hexagon has concurrent cross diagonals. What is the ratio of the product of the orange sides compared to the product of the purple sides. (ace:bdf).
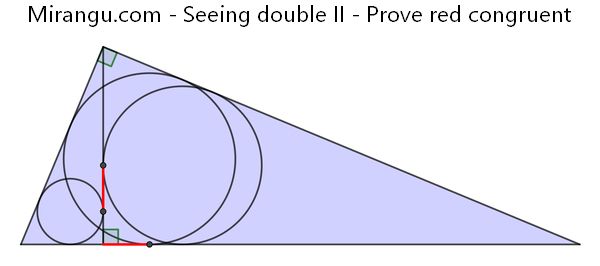
A right triangle is divided in two triangles by an altitude. The three incircles are shown with three tangency points. Prove that the two red line segments are congruent.
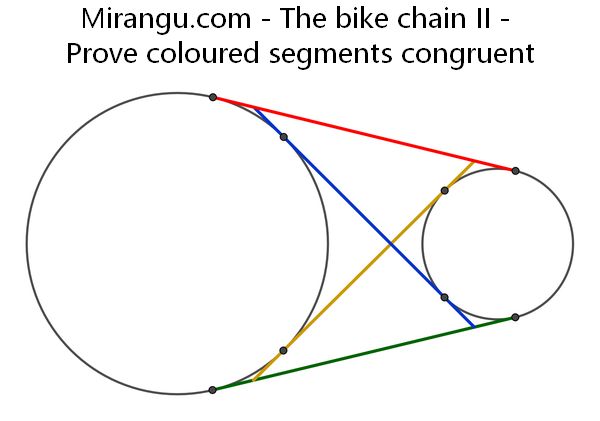
Two circles and four coloured common tangents. Prove they are congruent.
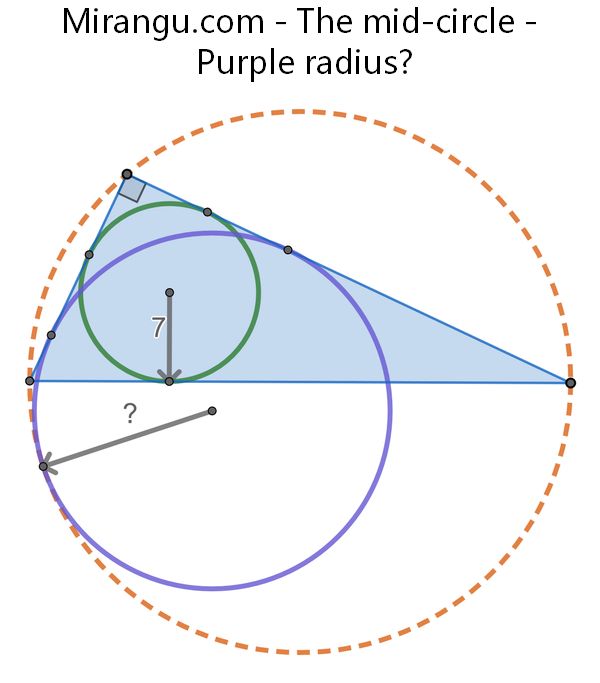
A blue right triangle has an orange-dotted circumcircle and a green incircle of radius 7. What is the radius of the purple circle, which is internally tangent to the orange circle and to the two sides of the right angle?
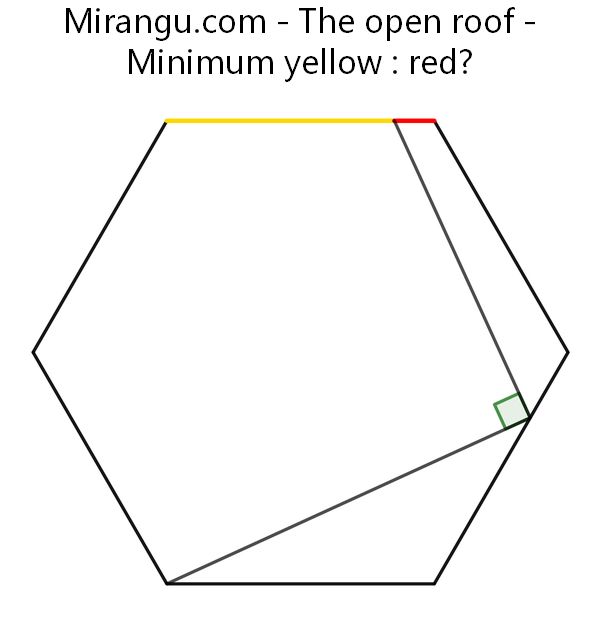
A regular hexagon with two line segments at right angles. What is the minimum of yellow : red?
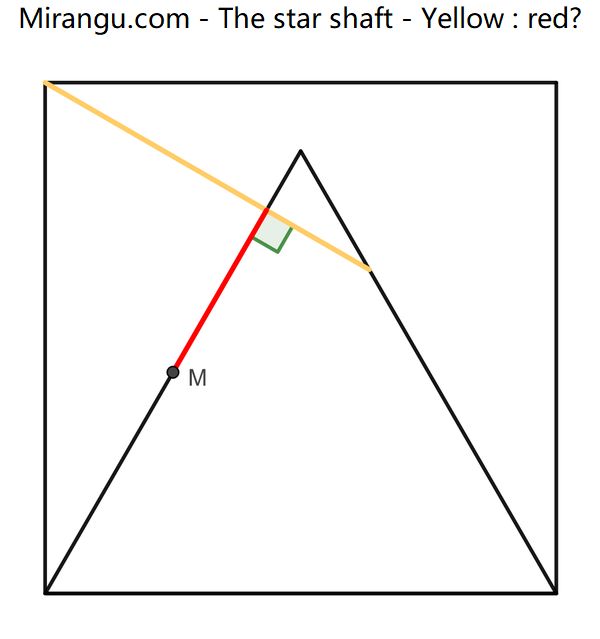
A square with an equilateral triangle. M is the triangle side midpoint. What is yellow : red?
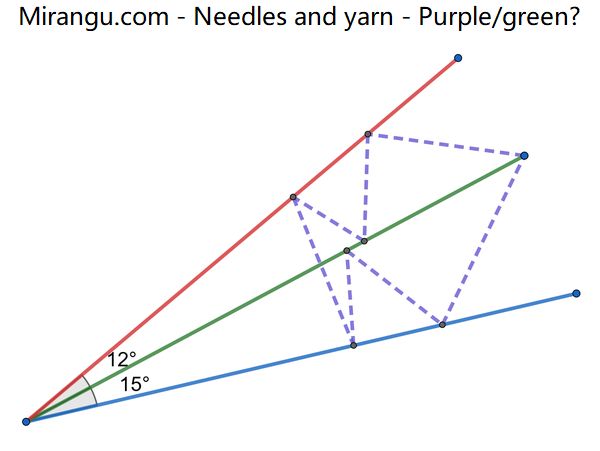
The purple yarn is stretched between the coloured needles approximately as shown, and the yarn is repositioned to make the shortest path of that type. What is the length ratio purple/green?
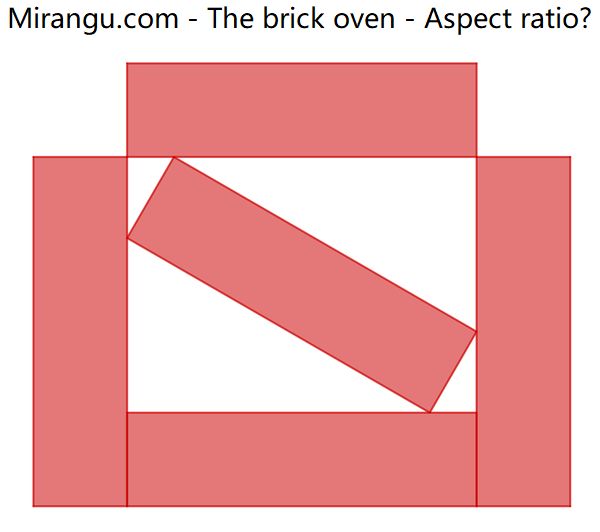
Five congruent rectangles. What’s their proportion width : height (aspect ratio)?