Several line segments, some of which are parallel. What is green : orange?
Euclid’s wing
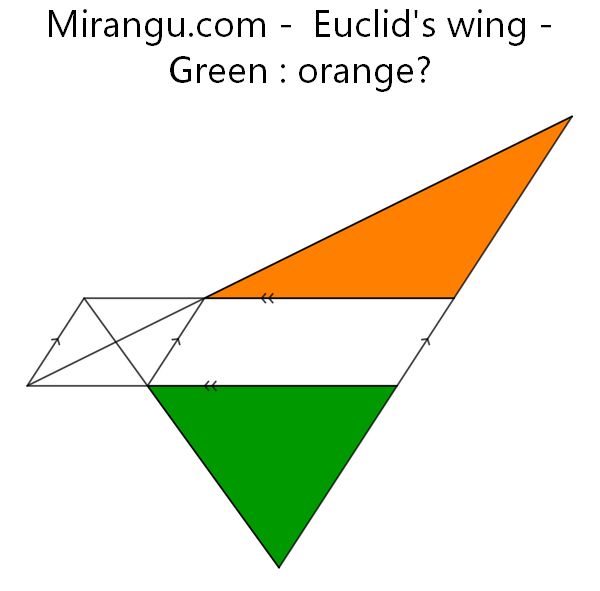

Several line segments, some of which are parallel. What is green : orange?
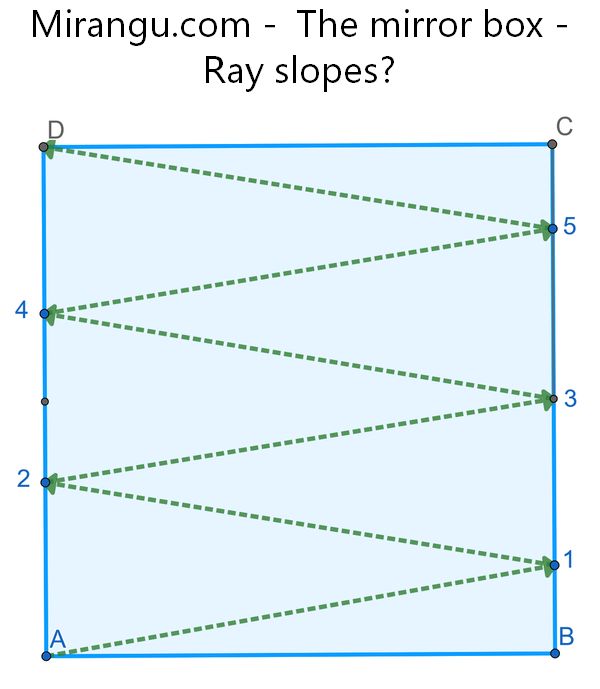
Light rays bounce off mirrored walls of a square before reaching one of the other corners. What are the slopes of the light rays leaving A that land in one of the corners B or D after exactly k=5 reflections?
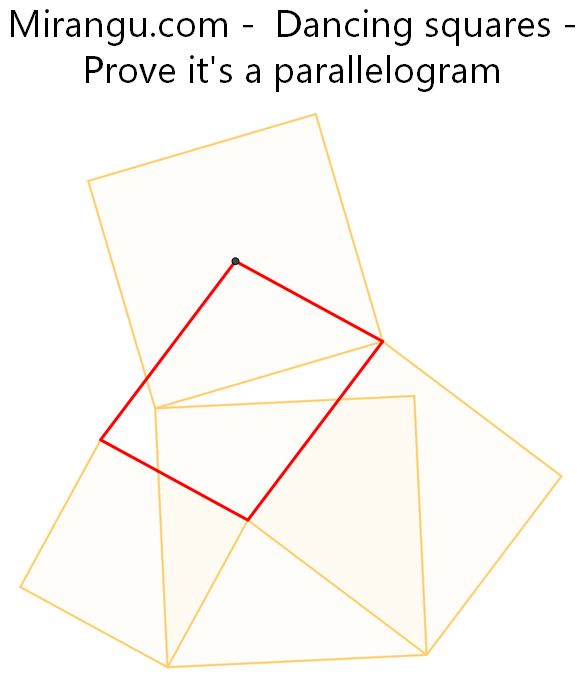
Four squares and one centre. Prove that the red quadrilateral is a parallelogram.
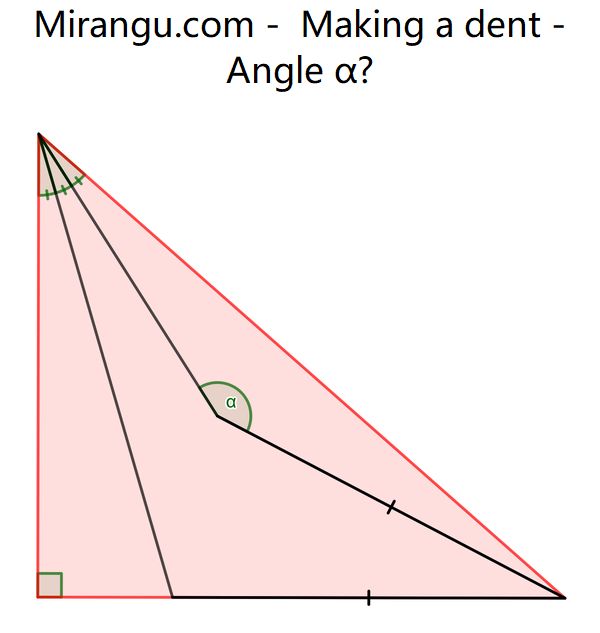
A right triangle with one trisected angle. What’s the angle α?
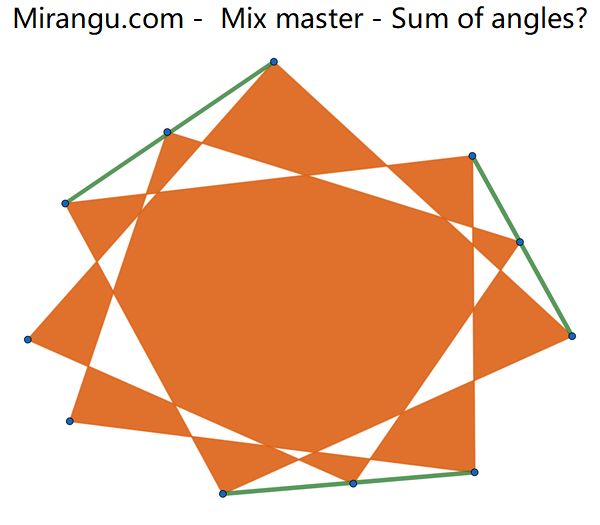
What is the sum of the angles at the blue vertices of this 11-gon?
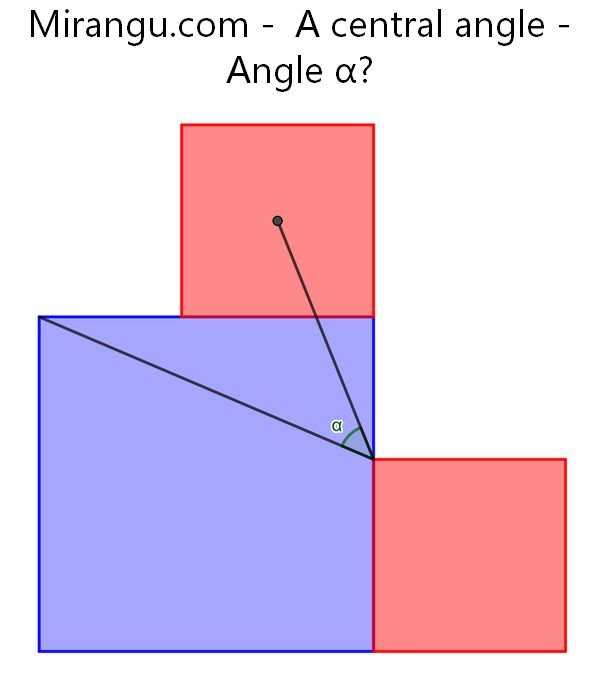
One blue and two congruent red squares. The shown point is the red square centre. What is the angle α?
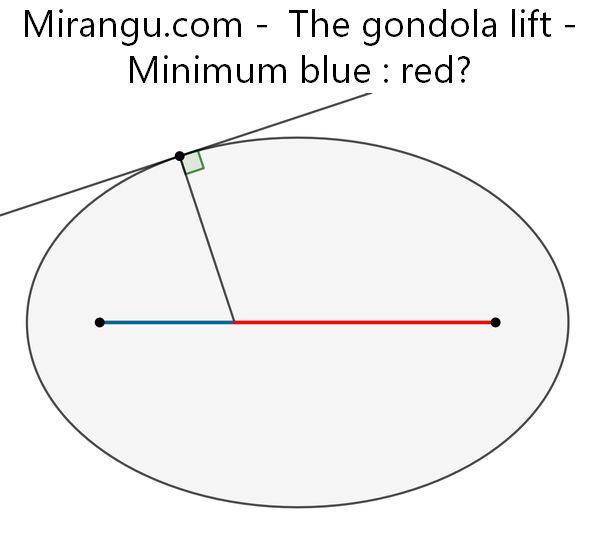
A tangent and its normal in an arbitrary point on an ellipse with eccentricity e. The focal points are also shown. What is the minimum value of blue : red in terms of e?
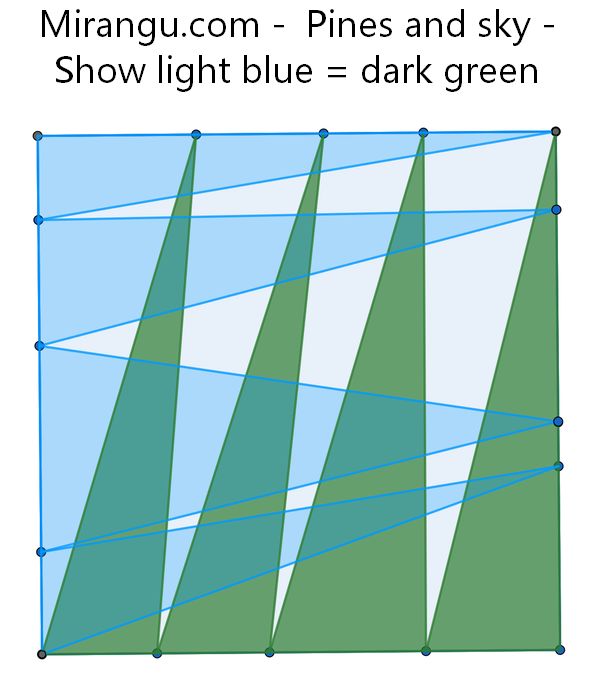
Show that the light blue area is the same as the dark green area.
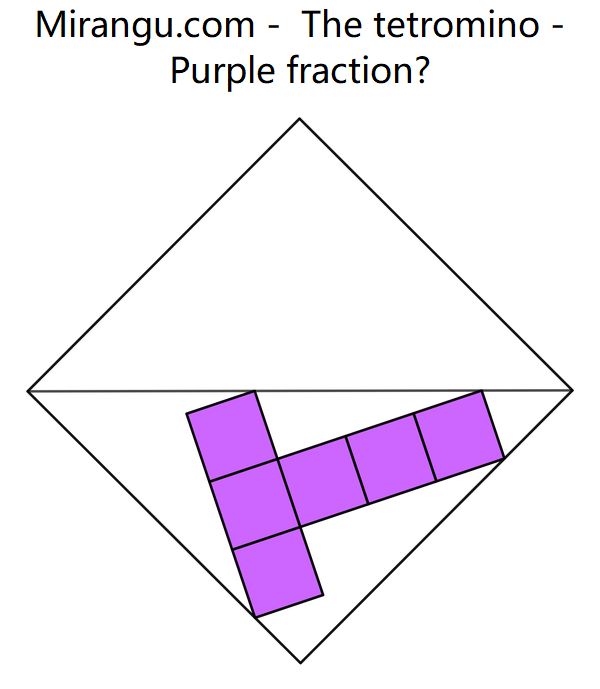
A square, its diagonal and six smaller squares. What fraction is purple?
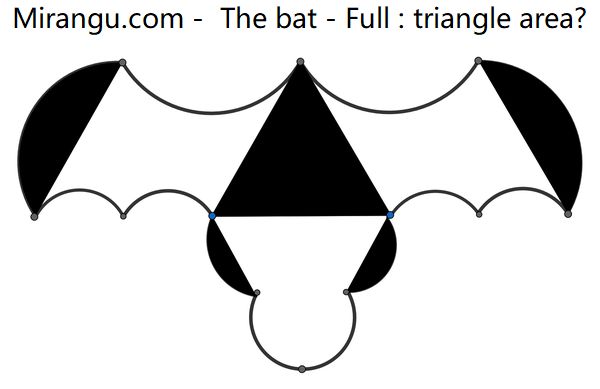
What is the full bat area (including the enclosed white parts) divided by that of its (equilateral triangular) upper torso?